SOLUBILITY OF THE HYDROXIDES, SULPHATES AND CARBONATES OF THE GROUP 2 ELEMENTS IN WATER

Go to the main page

This page looks at the solubility in water of the hydroxides, sulphates and carbonates of the Group 2 elements - beryllium, magnesium, calcium, strontium and barium. Although it describes the trends, there isn't any attempt to explain them on this page - for reasons discussed later. You will find that there aren't any figures given for any of the solubilities. There are major discrepancies between the figures given by two common UK A level Data Books (Nuffield Advanced Science Book of Data, and Chemistry Data Book by Stark and Wallace). There are also important inconsistencies within the books (one set of figures doesn't agree with those which can be calculated from another set). I haven't been able to find data which I am sure is correct, and therefore prefer not to give any. The FactsSolubility of the hydroxides The hydroxides become more soluble as you go down the Group. This is a trend which holds for the whole Group, and applies whichever set of data you choose. Some examples may help you to remember the trend: Magnesium hydroxide appears to be insoluble in water. However, if you shake it with water, filter it and test the pH of the solution, you find that it is slightly alkaline. This shows that there are more hydroxide ions in the solution than there were in the original water. Some magnesium hydroxide must have dissolved. Calcium hydroxide solution is used as "lime water". 1 litre of pure water will dissolve about 1 gram of calcium hydroxide at room temperature. Barium hydroxide is soluble enough to be able to produce a solution with a concentration of around 0.1 mol dm-3 at room temperature. Solubility of the sulphates The sulphates become less soluble as you go down the Group. The simple trend is true provided you include hydrated beryllium sulphate in it, but not if the beryllium sulphate is anhydrous. The Nuffield Data Book quotes anyhydrous beryllium sulphate, BeSO4, as insoluble (I haven't been able to confirm this from any other source), whereas the hydrated form, BeSO4.4H2O is soluble. (The Data Books agree on this - giving a figure of about 39 g dissolving in 100 g of water at room temperature.) Figures for magnesium sulphate and calcium sulphate also vary depending on whether the salt is hydrated or not, but nothing like so dramatically. Two common examples may help you to remember the trend: You are probably familiar with the reaction between magnesium and dilute sulphuric acid to give lots of hydrogen and a colourless solution of magnesium sulphate. Notice that you get a solution, not a precipitate. The magnesium sulphate is obviously soluble. You may also remember that barium sulphate is formed as a white precipitate during the test for sulphate ions in solution. The ready formation of a precipitate shows that the barium sulphate must be pretty insoluble. In fact, 1 litre of water will only dissolve about 2 mg of barium sulphate at room temperature. Solubility of the carbonates The carbonates tend to become less soluble as you go down the Group. None of the carbonates is anything more than very sparingly soluble. Magnesium carbonate (the most soluble one I have data for) is soluble to the extent of about 0.02 g per 100 g of water at room temperature. I can't find any data for beryllium carbonate, but it tends to react with water and so that might confuse the trend. The trend to lower solubility is, however, broken at the bottom of the Group. Barium carbonate is slightly more soluble than strontium sulphate. There are no simple examples which might help you to remember the carbonate trend. What - no explanations?Before I started to write this page, I thought I understood the trends in solubility patterns including the explanations for them. The more I have dug around to try to find reliable data, and the more time I have spent thinking about it, the less I'm sure that it is possible to come up with any simple explanation of the solubility patterns.

Note:  If you are interested in the reasons why I am unwilling to give the usual over-simplified explanations, I have described some of the problems as I see them on a separate page. That page also includes an attempt at a better explanation. Unless your syllabus specifically asks for explanations of these trends, you would be better off ignoring this follow-up page!

EXPLANATIONS FOR THE TRENDS IN SOLUBILITY OF SOME GROUP 2 COMPOUNDS This page looks at the usual explanations for the solubility patterns in the hydroxides, sulphates and carbonates of Group 2. It goes on to look at my misgivings about these. Don't expect this page to be easy - it is probably best avoided unless your syllabus specifically asks for these explanations!
	Warning:  If you have come straight to this page via a search engine, you should be aware that it is a follow-up to another page describing the solubility patterns. You should read that page before going on with this one.
The usual explanationsEnthalpy changes during the process The usual explanation is in terms of the enthalpy changes which occur when an ionic compound dissolves in water. Energy has to be supplied to break up the lattice of ions, and energy is released when these ions form bonds of one sort or another with water molecules.
	Note:  If you aren't happy about enthalpy changes, you might want to explore the energetics section of Chemguide, or my chemistry calculations book.
As you go down a Group, the energy needed to break up the lattice falls as the positive ions get bigger. The bigger the ions, the more distance there is between them, and the weaker the forces holding them together. Again as the positive ions get bigger, the energy released as the ions bond to water molecules (their hydration enthalpies) falls as well. Bigger ions aren't so strongly attracted to the water molecules. Since both of these important enthalpy terms fall as you go down the Group, what matters in deciding whether the change becomes more endothermic or more exothermic overall is how fast they fall relative to each other. A sample calculation to make this clear Here is an example of the sort of calculations you might do to work out the enthalpy change of solution for sodium chloride and potassium chloride.
	Note:  You may wonder why I haven't used an example directly relevant to the hydroxides, sulphates or carbonates of Group 2. I tried doing this with figures (taken from a variety of sources) for carbonates, but got answers for enthalpy changes of solution which didn't bear the slightest resemblance to the actual values quoted in a data book. I have no idea why! Doing the sums with Group 1 chlorides does give (fairly) accurate results, and the methods and discussion applies equally well to the Group 2 compounds we are interested in.The data used comes from Chemistry Data Book by Stark and Wallace. The Nuffield Data Book doesn't have any hydration enthalpy values.
In this case, we are defining lattice enthalpy as the heat needed to convert 1 mole of crystal in its standard state into separate gaseous ions - an endothermic change.
	Note:   Lattice enthalpy is more usually defined in the opposite direction - as the heat evolved when the lattice is formed from its gaseous ions. Defining it in the endothermic direction makes the argument a bit easier in this particular case. This endothermic change involving the break up of the lattice is properly called "lattice dissociation enthalpy", although the simpler term "lattice enthalpy" is still often used for it.
You can see that the enthalpy of solution changes from NaCl to KCl because the lattice enthalpy and hydration enthalpy of the positive ion fall by different amounts. If the hydration enthalpy falls faster than the lattice enthalpy (as in this case), the net effect is that the overall change becomes more endothermic (or less exothermic in other possible cases where the total enthalpy change turns out to be negative). If the lattice enthalpy falls faster than the hydration enthalpy, the opposite happens - the change will become less endothermic (or more exothermic). What controls the relative rate of fall of the two terms? 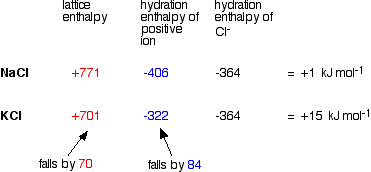It turns out that the main factor is the size of the negative ion. For small negative ions like hydroxide, the lattice enthalpy falls faster than the hydration enthalpy of the positive ions. That means that the enthalpy of solution will become less positive (or more negative). For large negative ions like sulphate or carbonate, the hydration enthalpy of the positive ions falls faster than the lattice enthalpy. In this case, the enthalpy of solution will become more positive (or less negative). Why the difference? Lattice enthalpy is governed by several factors - including the distance between the negative and positive ions. Where you have a big negative ion, this inter-ionic distance is largely controlled by the size of that negative ion. Changes in the size of the positive ion don't make as great a percentage difference to the inter-ionic distance as they would if the negative ion was small. With sulphates, for example, the percentage increase in the inter-ionic distance as you go from magnesium to calcium sulphate isn't as great as it would be with a smaller negative ion like hydroxide. Since the percentage increase in inter-ionic distance isn't very great, the change in the lattice enthalpy won't be very great either. The relationship between enthalpy of solution and solubility The assumption is made that the more endothermic (or less exothermic) the enthalpy of solution is, the less soluble the compound. So sulphates and carbonates become less soluble as you go down the Group; hydroxides become more soluble. Problems with the usual explanationsProblems with the data Unfortunately, the enthalpy of solution values for the Group 1 chlorides as calculated above don't agree with the values given in the same Data Book: Calculated value (kJ mol-1) Data book value (kJ mol-1) NaCl +1 +3.9 KCl +15 +17.2 RbCl +10 +16.7 CsCl +5 +17.9 The discrepancies are enough to disrupt any pattern (such as there is!). The reasons for the discrepancies lie in the way the numbers are calculated. These are very small numbers worked out from much larger ones. Small uncertainties in those large numbers will cause large swings in the answers. For example, if each of the numbers in the calculations we did earlier on this page was out by just 5 kJ, each answer could vary by +/- 15 kJ - completely disrupting the patterns! You can't therefore reliably use the data available to calculate the trends you want with sufficient accuracy to make sense. Problems correlating enthalpy data with the facts The solubilities of the Group 1 chlorides (in moles of solute saturating 100 g of water at 298 K) compared with their enthalpies of solution are: Enthalpy of solution (kJ mol-1) Solubility (mol /100 g of water) NaCl +3.9 0.615 KCl +17.2 0.481 RbCl +16.7 0.781 CsCl +17.9 1.13 There is no obvious relationship connecting the relative movements of these solubility values with the enthalpy of solution figures. It would be quite untrue to say that the more endothermic the change, the less soluble the compound! Problems in relating the sign of the enthalpy change to solubility The table above illustrates this problem, but it gets worse! Taking the sign of enthalpy of solution at face value, you get some bizarre results. The enthalpy of solution figures for the Group 2 carbonates are: (source: Chemistry Data Book by Stark and Wallace; values in kJ mol-1) MgCO3 -25.3 CaCO3 -12.3 SrCO3 -3.4 BaCO3 +4.2 Sodium chloride and the other Group 1 chlorides dissolve despite the fact that their enthalpies of solution are positive, and yet magnesium carbonate (and most of the other Group 2 carbonates) are very sparingly soluble, but have exothermic enthalpies of solution. You might have expected exactly the opposite to happen. However if you ignore the comparison with the Group 1 chlorides, you could argue that the figures get progressively less exothermic, and at barium carbonate become endothermic. That would seem to support the decrease in solubility as you go down the Group quite nicely. Unfortunately, if you look at the solubility data, the trend is broken at the bottom of the Group. Barium carbonate is more soluble than strontium carbonate! Although figures from my two data sources differ in detail, they agree on this. Clearly, trying to correlate solubility simply with the enthalpy change of solution doesn't work. Introducing entropy changesThe basic explanation To get around the problem of many compounds dissolving freely in water despite the fact that their enthalpies of solution are endothermic you have to introduce the concept of entropy change. The only way of making sense of entropy without getting bogged down in some serious maths is to think of it as a measure of the amount of disorder in a system. Entropy is given the symbol S. If a system becomes more disordered, then its entropy increases. In order to see whether a change is possible or not, you have to think about a combination of the enthalpy change and the entropy change. These can be combined mathematically to give an important term known as free energy change. 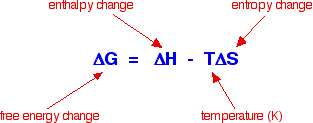As an approximation, for a reaction to happen, the free energy change must be negative. What happens if the enthalpy change is positive - as for example when sodium chloride dissolves in water (+3.9 kJ mol-1, using the values in one of the tables above)? As long as the entropy change is positive enough, it is possible to get a negative value for free energy change. In the sodium chloride case, you don't have to have very much increase in entropy to outweigh the small enthalpy change of +3.9 kJ mol-1. So . . . does the entropy increase when sodium chloride dissolve in water? Yes, it does! Originally, the sodium and chloride ions were arranged in a very tidy way in the crystal lattice - their entropy was low. (Remember that entropy is a measure of disorder.) When you dissolve the crystal in water, the entropy increases as the ions and water molecules become completely jumbled up - they become much more disordered than they were originally. This is where the explanation usually stops, but to stop at this point is very misleading because it won't explain all the facts! What's wrong with this explanation? The most obvious thing that's wrong is that it won't explain why some compounds (like magnesium carbonate, and most of the other Group 2 carbonates) don't dissolve in water even though their enthalpies of solution are mainly negative. In these cases, the entropy of the system must fall when the compounds dissolve in water - in other words, the solution in water is more ordered than the original crystal and water! 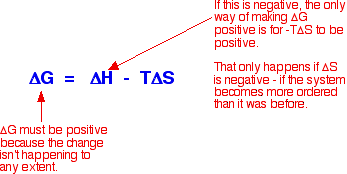This happens because the water molecules become more ordered when the compound dissolves in them. Instead of milling around pretty much at random, they become attracted to the ions present and arranged around them. This is particularly effective if the ions are small and highly charged - and so the effect is greatest for the positive ions at the top of the Group, and gets less as you go down. It is also much more important in Group 2 than in Group 1 where the ions only carry one positive charge. That means that you have two entropy effects to consider. There is the increase in disorder as the crystal lattice breaks up, but a corresponding increase in order in the water - which varies depending on the sizes and charges of the ions present. What a nightmare! To explain this properly, you need to think about the way lattice enthalpy changes as you go down the Group, the way that hydration enthalpies change, and the way that entropy changes. The way those changes happen will vary from one type of compound to another. Can we explain everything now? No - at least not easily! For example, although it might be possible to account for the lack of pattern in the solubilities of the Group 1 chlorides (and also the bromides) by a mathematical application of these effects, trying to do it in general terms defeats me completely! You could, however, make a reasonable suggestion as to why the solubility trend in the carbonates is broken at barium. (Don't expect the explanation to be instantly understandable though!) Remember that the solubility of the carbonates falls as you go down Group 2, apart from an increase as you go from strontium to barium carbonate. The general fall is because hydration enthalpies are falling faster than lattice enthalpies. Remember that where you have a big negative ion, its size dominates the inter-ionic distance and so doesn't allow the lattice enthalpy to change much. This gives the enthalpy of solution values we've already looked at (values in kJ mol-1): MgCO3 -25.3 CaCO3 -12.3 SrCO3 -3.4 BaCO3 +4.2 But the entropy change will also be varying as you go down the Group. At the top, where you have small 2+ ions, the overall entropy change in the system must be negative - the system as a whole becomes more ordered when the compound dissolves because of the way the water molecules become organised around the positive ions. That negative entropy change is going to be enough to wipe out the effect of the exothermic enthalpy of solution.
	Note:  You need to think about the effect of the positiveness and negativeness of these values on the size of the free energy change. Use the equation further up this page.
Towards the bottom of the Group, this effect changes. The bigger ions have less organising effect on the water molecules. The entropy change is becoming less negative (or perhaps even at this stage, positive). That's going to tend to make the compounds more soluble. The overall effect is a complex balance between the way the enthalpy of solution varies and the way the entropy change of solution alters. At barium carbonate, the effect of increasing entropy must be enough to make it more soluble than strontium carbonate.
	A personal comment:  I see it as quite wrong that this should be discussed at this level (UK A level or its equivalent). The usual explanations are over-simplistic and potentially misleading - especially for anyone who might go on to do Chemistry at degree level. Fortunately most syllabuses have enough sense not to ask for these explanations!Science progresses by offering theories which have to explain all the facts. Where a fact won't fit a theory, the theory has to be modified, or even discarded. What we seem to be doing here is presenting students with an inadequate theory and then ignoring all the facts which don't fit it. I see that as quite dangerous. It would be much better not to discuss this at all at this level, rather than to give students a false view of the way science works.